ANSWER
R2 = 2R1
The range of the second projectile is two times the range of the first projectile.
Step-by-step explanation
The gun is always in the same position and two projetiles are fired at different speeds:
Because the gun is in the same position above the floor and for both projectiles the initial vertical speed is 0 both projectiles are in the air the same time t.
The range for each projectile is
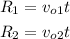
And we know that the speed of the second projectile is twice the speed of the first projectile:

Replace this into the equation of the range of the second projectile
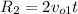
And note that next to the 2 coefficient there's the equation for the range of projectile 1:

Therefore the range of the second projectile is two times the range of the first projectile.