Question

1.Write a matrix representing the system of equations3x+5y=20-x+y= - 4Solve the system by transforming your matrix into reduced row echelon form. State the solution as an ordered triple.

Answer 1

The augmented matrix which represents the system of equations is

`\begin{bmatrix}{3} & {5} & {20} \\ {-1} & {1} & {-4} \\ {} & {} & {}\end{bmatrix}`

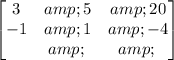
Now, lets solve the system by reducing this matrix to row echelon form.

By dividing the first row by 3, we have

`\begin{bmatrix}{1} & {(5)/(3)} & {(20)/(3)} \\ {-1} & {1} & {-4} \\ {} & {} & {}\end{bmatrix}`

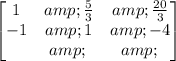
Now, by adding the rows, we get

`\begin{bmatrix}{1} & {(5)/(3)} & {(20)/(3)} \\ {0} & {(8)/(3)} & {(8)/(3)} \\ {} & {} & {}\end{bmatrix}`

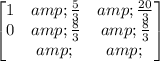
By multiplying the second row by 8/3, we have

`\begin{bmatrix}{1} & {(5)/(3)} & {(20)/(3)} \\ {0} & {1} & {1} \\ {} & {} & {}\end{bmatrix}`

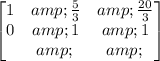
and by multiplying the second row by -5/3, we get

`\begin{bmatrix}{1} & {(5)/(3)} & {(20)/(3)} \\ {0} & {-(5)/(3)} & {(5)/(3)} \\ {} & {} & {}\end{bmatrix}`

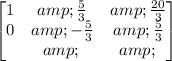
and by adding the second row to the first rwo, we obtain

`\begin{bmatrix}{1} & {0} & {(15)/(3)} \\ {0} & {1} & {1} \\ {} & {} & {}\end{bmatrix}`

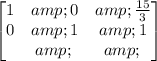
therefore, the final result is

`\begin{bmatrix}{1} & {0} & {5} \\ {0} & {1} & {1} \\ {} & {} & {}\end{bmatrix}`

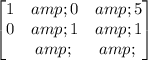
This means that the solution is x=5 and y=1. Then, the solution is (5,1)