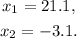Question

Solve do x by completing the square ten round to nearest tenth

Answer 1

To complete the square means that by adding or subtracting a constant to the equation, we have to take the left side of the equation to the form:

`(x-k)^2=x^2-kx+k^2\text{.}`

Now, notice that:

`18x=2(9)x\text{.}`

Adding 81=9² to the equation we get:

`x^2-18x+81=65+81.`

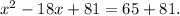
Therefore, we can rewrite the given equation as:

`(x-9)^2=146.`

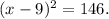
Then:

`x-9=\pm\sqrt[]{146}.`

Finally, we get that:

`x=9\pm\sqrt[]{146}.`

Answer:

`\begin{gathered} x_1=21.1, \\ x_2=-3.1. \end{gathered}`