Answer:
The radius of the Hemisphere is 15.8 cm.
![r=15.8\operatorname{cm}]()
Step-by-step explanation:
The formula for the volume of an hemisphere can be written as;
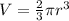
Given that the volume of the hemisphere is;
![8231\operatorname{cm}^3]()
We can get the radius of the hemisphere using the formula above.
Firstly let us make r the subject of formula;
![\begin{gathered} V=(2)/(3)\pi r^3 \\ \text{multiply through by 3/2} \\ (3)/(2)V=\pi r^3 \\ \text{divide through by pi} \\ (3)/(2)(V)/(\pi)=r^3 \\ \text{cube root both sides} \\ \sqrt[3]{(3)/(2)(V)/(\pi)}=r \\ r=\sqrt[3]{(3)/(2)(V)/(\pi)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/k0cfaporyyaupd0tdott4oc6ht13hdarho.png)
Lastly let us substitute the given volume V into the derived formula for radius r.
![\begin{gathered} r=\sqrt[3]{(3)/(2)(V)/(\pi)} \\ r=\sqrt[3]{(3*8231)/(2*\pi)}=\sqrt[3]{(24693)/(2*\pi)} \\ r=15.78\operatorname{cm} \\ r=15.8\operatorname{cm}\ldots\ldots.(to\text{ the nearest tenth of a centimeter)} \end{gathered}]()
Therefore, the radius of the Hemisphere is 15.8 cm.
![r=15.8\operatorname{cm}]()