Question

Help please this is not a quiz I need help I’m practicing and I don’t understand

Answer 1

Since the height of the freefall is parabolic as shown below,

the standard form of expressing a parabola is given as

`\begin{gathered} y=a(x-h)^2+k\text{ ----- equation 1} \\ \text{where} \\ (h,k)\text{ is the coordinate of the vertex of the parabola} \end{gathered}`

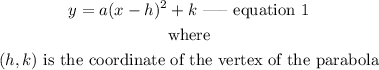
Step 1: Evaluate the coordinate of the vertex of the parabola.

In the above graph, the coordinate of the vertex is (0,0).

Thus,

`\begin{gathered} h=0 \\ k=0 \end{gathered}`

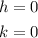
Step 2: Substitute the values of h and k into equation 1.

Thus,

`\begin{gathered} y=a(x-h)^2+k \\ h=0,\text{ k=0} \\ y=a(x-0)^2+0 \\ \Rightarrow y=ax^2\text{ ----- equation 2} \end{gathered}`

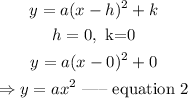
Step 3: Select a point on the curve, and substitute the values of x and y into equation 2, to obtain a.

Thus, using the point (0.2, -3) as shown above, where x=0.2 and y=-3, we have

`\begin{gathered} y=ax^2 \\ x=0.2,\text{ y=-3} \\ \Rightarrow-3=a(0.2)^2 \\ -3=0.04a \\ \Rightarrow a=-(3)/(0.04) \\ a=75 \end{gathered}`

Substitute the value of a into equation 2.

Thus,

`\begin{gathered} y=75x^2 \\ \text{where} \\ y\Rightarrow h(d) \\ x\Rightarrow d \end{gathered}`

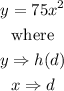
Hence, the function that describes these coordinates is expressed as

`h(d)=75d^2`