Answer:
31/32
Explanation:
If a coin is tossed 5 times, obtaining at least 1 tail means you can either obtain 1,2,3,4, or 5 tails.
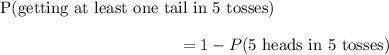
In a coin toss:

Therefore:
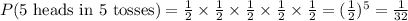
This then means that the probability of getting at least 1 tail:
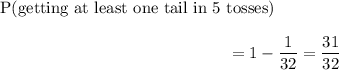
The probability is 31/32.
Note: You can also solve this problem using the binomial probability formula.