Question

5. During the summer, you want to earn $250 each week. Du earn $10 per hour working as alifeguard and $8 per hour at the concession stand. You are only available to work 30 total hours eachweek. Which system of equations matches this scenario?A. x + y = 250, 18x 30B. x + y = 250, 10x + 8y = 30--C. x + y = 30, 10x + 8y = 250D. 10x + 8y = 250, 10x + 8y = 30

Answer 1

write out the information given,

`\begin{gathered} \text{Total amount to earn = \$250} \\ \text{Total hours worked we}ekly=30 \end{gathered}`

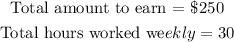
Also

`\begin{gathered} \text{earn \$10per hours in lifeguard} \\ \text{Earn \$8 per hour in concession stand} \end{gathered}`

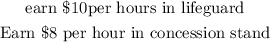
Defina a parameter for the number of hours worked in each company

`\begin{gathered} \text{Let} \\ \text{Hours work at lifeguard=x,} \\ Hours\text{ work at Consession stand=y} \end{gathered}`

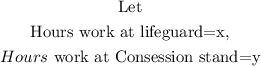
Since the total hours worked is 30, we have

`x+y=30`

The amount received from each company will be hours worked multiplied by the pay per hours.

hence

`\begin{gathered} \text{for lifeguard,} \\ =10* x=10x \\ \text{for concession stand} \\ =8* x=8x \end{gathered}`

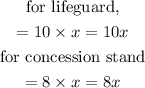
Since the total amount to you want is $ 250, then

`10x+8x=250`

Therefore

The system of equation for the scenario is

x+y = 30, 10x+ 8x = 250

Answer is Option C