Answer:
37 years
Explanation:
When interest is being compounded continuously, we use the below compound interest formula;
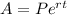
where A = future value of the investment
P = principal amount (initial investment)
r = interest rate in decimal
t = time in years
From the question, we're told that the future value(A) of the initial investment amount(P) will be triple, so we have that A = 3P.
Also, we're given an interest rate of 3%, so r = 3/100 = 0.03
Let's substitute these values into our formula;
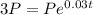
We'll follow the below steps to solve for t;
Step 1: Divide both sides by P;
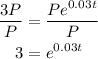
Step 2: We'll now take the natural logarithm of both sides;

Step 3: Divide both sides by 0.03;
