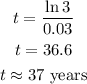Question

How long will it take for an investment to triple, if interest is compounded continuously at 3%?

Answer 1

37 years

Explanation:

When interest is being compounded continuously, we use the below compound interest formula;

`A=Pe^(rt)`

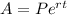
where A = future value of the investment

P = principal amount (initial investment)

r = interest rate in decimal

t = time in years

From the question, we're told that the future value(A) of the initial investment amount(P) will be triple, so we have that A = 3P.

Also, we're given an interest rate of 3%, so r = 3/100 = 0.03

Let's substitute these values into our formula;

`3P=Pe^(0.03t)`

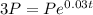
We'll follow the below steps to solve for t;

Step 1: Divide both sides by P;

`\begin{gathered} (3P)/(P)=(Pe^(0.03t))/(P)^{} \\ 3=e^(0.03t) \end{gathered}`

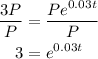
Step 2: We'll now take the natural logarithm of both sides;

`\begin{gathered} \ln 3=\ln (e^(0.03t)) \\ \ln 3=0.03t\ln e \\ \text{Note that ln e = 1} \\ \ln 3=0.03t \end{gathered}`

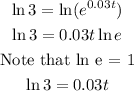
Step 3: Divide both sides by 0.03;

`\begin{gathered} t=(\ln 3)/(0.03) \\ t=36.6 \\ t\approx37\text{ years} \end{gathered}`