Given the following expression:
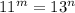
Solving :
![\sqrt[n]{11^m}=\sqrt[n]{13^n}](https://img.qammunity.org/2023/formulas/mathematics/college/quoi7hq0bogd2jjz5anai4w7137jv9ip9b.png)
![\sqrt[n]{11^m}=13](https://img.qammunity.org/2023/formulas/mathematics/college/uthzsnibgay7grnagmrp2qjkq8scbq4h1b.png)
We can write the root in the following way:
![\sqrt[n]{11^m}=11^{(m)/(n)}](https://img.qammunity.org/2023/formulas/mathematics/college/k95sxy1gotke5fombdi98cyqh70nufg685.png)
Therefore:
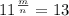
If m>n :
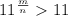
If m
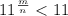 Therefore, m have to be greater than n.
Therefore, m have to be greater than n.
Finally: if m and n are integers:
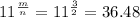
To get a value equal to 13, n has to be close to m, otherwise the number will be very large.
In this case: (Using the same numbers of the example):
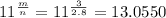
Answer: It is impossible to find non-zero integer numbers, because m or n have to be a rational number.