Question

"Is it possible to find nonzero whole numbers m and n such that 11^m = 13^n? Explain."

Answer 1

Given the following expression:

`11^m=13^n`

Solving :

`\sqrt[n]{11^m}=\sqrt[n]{13^n}`
`\sqrt[n]{11^m}=13`

We can write the root in the following way:

`\sqrt[n]{11^m}=11^{(m)/(n)}`

Therefore:

`11^{(m)/(n)}=13`

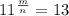
If m>n :

`11^{(m)/(n)}>11`

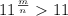
If m
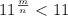`11^{(m)/(n)}<11`Therefore, m have to be greater than n.

Finally: if m and n are integers:

`11^{(m)/(n)}=11^{(3)/(2)}=36.48`

To get a value equal to 13, n has to be close to m, otherwise the number will be very large.

In this case: (Using the same numbers of the example):

`11^{(m)/(n)}=11^{(3)/(2.8)}=13.0550`

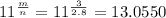
Answer: It is impossible to find non-zero integer numbers, because m or n have to be a rational number.