Question

Mark owes $12,000 on two loans. The interest rate on the first loan is 8% and the interest rate on the second loan was 9%. The total amount of interest he has paid in one year is $1,010. What was the principal for each loan?

Answer 1

Let x be the principal of the first loan, and y be the principal of the second loan, then, we can set the following system of equations:

`\begin{gathered} x+y=12,000, \\ 0.08x+0.09y=1,010. \end{gathered}`

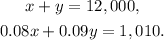
Solving the first equation for x, we get:

`x=12,000-y\text{.}`

Substituting the above result in the second equation, we get:

`0.08(12,000-y)+0.09y=1,010.`

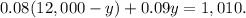
Solving the above equation for y, we get:

`\begin{gathered} 960-0.08y+0.09y=1,010, \\ 0.01y=1,010-960, \\ 0.01y=50, \\ y=5000. \end{gathered}`

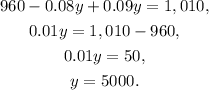
Substituting y=5000, in x=12,000-y, we get:

`x=12,000-5000=7000.`

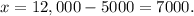
Answer:

The principal of the 8% interest loan was $5000, and the principal of the other loan was $7000.