Given the mass of the ball, m= 6 kg, and the horizontal speed, v = 60 m/s.
Also, the height of the platform, h = 80 m
(a) To find the time required to reach the ground, t
Time can be calculated from the formula
![\begin{gathered} h=(1)/(2)gt^2 \\ t=\sqrt[]{(2h)/(g)} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/oe7enbxzshecmxg5oyzrjyjfzsfy41vygb.png)
Here, g= 9.8 m/s^2 which is the acceleration due to gravity.
Substituting the values in the above equation, we get
![\begin{gathered} t=\sqrt[]{(2*80)/(9.8)} \\ =4.03\text{ seconds} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/jb93mzkg0l03t4xunvjyyxfpqy0oczgv6d.png)
(b) To find the Kinetic energy of the ball.
In order to find kinetic energy, first, we need to find the velocity.
The velocity at the ground, u can be obtained by the formula
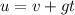
Substituting the values, we get
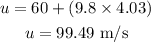
Substituting the value of velocity in the below formula of kinetic energy, we get
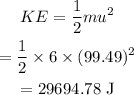
Thus, the time taken is 4.03 seconds and kinetic energy is 29694.78 J