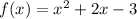
In order to determine the zeros of this function, the steps are:
1. Assume f(x) = 0. Hence, the equation becomes:
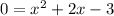
2. Factor the quadratic function by finding some factors of -3 that sums to the middle term 2.
a. -3 and 1 → -2
b. -1 and 3 → 2
So, the factors of -3 that sums to 2 are -1 and 3.
So, the quadratic equation can be factored into:
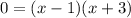
3. Equate each factor to zero and solve for x.
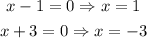
Therefore, the zeroes of the function are at (-3, 0) and (1, 0). (Option C)