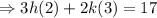Question

I need to find the value of sum and difference functions

Answer 1

The functions are given below as

`\begin{gathered} h(x)=x^2+1 \\ k(x)=x-2 \end{gathered}`

Step 1:

To figure out the (h+k)(2), we will use the formula below

`(h+k)(x)=h(x)+k(x)`

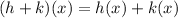
By substituting the values, we will have

`\begin{gathered} (h+k)(x)=h(x)+k(x) \\ (h+k)(x)=x^2+1+x-2 \\ (h+k)(x)=x^2+x-1 \\ (h+k)(2)=2^2+2-1 \\ (h+k)(2)=4+2-1 \\ (h+k)(2)=5 \end{gathered}`

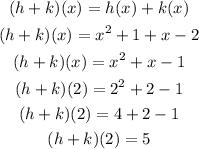
Hence,

The final answer is

`\Rightarrow(h+k)(2)=5`

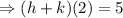
Step 2:

To figure out the (h-k)(3), we will use the formula below

`\begin{gathered} (h-k)(x)=h(x)-k(x) \\ \end{gathered}`

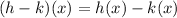
By substituting the values, we will have

`\begin{gathered} (h-k)(x)=h(x)-k(x) \\ (h-k)(x)=x^2+1-(x-2) \\ (h-k)(x)=x^2+1-x+2 \\ (h-k)(x)=x^2-x+3 \\ (h-k)(3)=3^2-3+3 \\ (h-k)(3)=9 \end{gathered}`

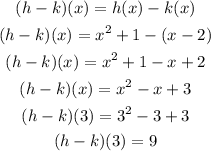
Hence,

The final answer is

`\Rightarrow(h-k)(3)=9`

Step 3:

To figure out the value of 3h(2) +2k(3), we will use the formula below

`\begin{gathered} 3h(x)+2k(x)=3(x^2+1)+2(x-2) \\ 3h(2)=3(2^2+1)=3(4+1)=3(5)=15 \\ 2k(3)=2(x-2)=2(3-2)=2(1)=2 \\ 3h(2)+2k(3)=15+2=17 \end{gathered}`

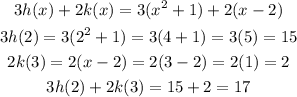
Hence,

The final answer is

`\Rightarrow3h(2)+2k(3)=17`