Answer:
A. There is only one possible solution for this triangle.
• B=8 degrees
,
• C=152 degrees
• c=13.7
Explanation:
Given the following measurements in a triangle ABC:
• a=10
,
• b = 4
,
• A=20°
Since the given angle A is opposite the longer side, the given measurements will produce one triangle.
(a)First, find the value of angle B using the Law of Sines.

(b)Next, find the value of angle C.
The sum of the measures of angles in a triangle is 180 degrees, therefore:
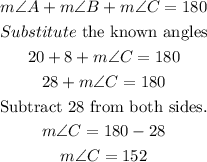
(c)Here we find the value of side length c.
Using the Law of Sines:.

The values of B, C, and c are 8 degrees, 152 degrees, and 13.7 respectively.
The correct option is A.