Question

identify the key features of the parabola that is formed by the equationf (x) = -4.9x² + 19.8x + 58 round the answer to the nearest whole number 1- the x-intercepts2- the y-intercept3- the vertex4- is the vertex a maximum/minimum

Answer 1

To find the x-intercepts, equal the equation to 0 and solve for x:

-4.9 x^2 + 19.8x + 58

ax^2 + bx + c

a = -4.9

b= 19.8

c= 58

Apply the quadratic formula:

`\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}`
`\frac{-19.8\pm\sqrt[]{19.8^2-4\cdot-4.9\cdot58}}{2\cdot-4.9}`
`\frac{-19.8\pm\sqrt[]{392.04+1,136.8}}{-9.8}`
`(-19.8\pm39.10)/(-9.8)`

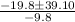
positive : -1.97

negative : 6.01

• 1- x intercepts

x = -1.97 , x = 6.01

• 2.y-intercept

To find it replace x = 0 and solve for y:

y = -4.9x^2 + 19.8x + 58

y= -4.9 (0)^2 + 19.8 (0) + 58

y= 58

• 3. Vertex

First, find the axis of symmetry:

x = -b / 2*a = -19.8 / 2*-4.9 = 2.02

Replace x=2.02 on the equation:

y = -4.9 (2.02)^2 + 19.8 (2.02) + 58

y = -19.99 + 39.996 + 58

y = 78

Vertex = (2.02 , 78 )

4.

Since on x-intercept is at x=-1.97, replace x=-3 and see if the y value is positive or negative:

f(-3) = -4.9(-3)^2 + 19.8 (-3) + 58

f(-3)= -44.1 -59.4 +58

f(-3)= -45.5

Since the value is negative it opens downwards, so the vertex is a maximum.

Answers:

1- the x-intercepts

x = -1.97 , x = 6.01



2- the y-intercept

y= 58



3- the vertex

Vertex = (2.02 , 78 )



4- is the vertex a maximum/minimum​

The vertex is a maximum