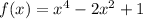
To solve the real zeros in this given function above, let's factor out the function.
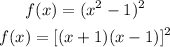
With the given factors, the real zeros are when x = 1, and x = -1.
Let's try to check if f(x) = 0 if x = 1, and x = -1 to see if we are right.
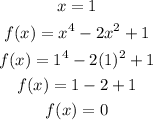
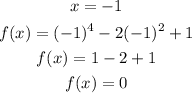
Indeed, x = 1 and x = -1 are the zeros of the given function and they only appear once. Therefore, the multiplicity of each factor is 1.
The graph of the function is also shown below: