Question

Find the real zeros and state their multiplicity: ()=^4−2^2+1

Answer 1

`f(x)=x^4-2x^2+1`

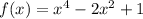
To solve the real zeros in this given function above, let's factor out the function.

`\begin{gathered} f(x)=(x^2-1)^2 \\ f(x)=\lbrack(x+1)(x-1)\rbrack^2 \end{gathered}`

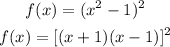
With the given factors, the real zeros are when x = 1, and x = -1.

Let's try to check if f(x) = 0 if x = 1, and x = -1 to see if we are right.

`\begin{gathered} x=1 \\ f(x)=x^4-2x^2+1 \\ f(x)=1^4-2(1)^2+1 \\ f(x)=1-2+1 \\ f(x)=0 \end{gathered}`
`\begin{gathered} x=-1 \\ f(x)=(-1)^4-2(-1)^2+1 \\ f(x)=1-2+1 \\ f(x)=0 \end{gathered}`

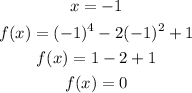
Indeed, x = 1 and x = -1 are the zeros of the given function and they only appear once. Therefore, the multiplicity of each factor is 1.

The graph of the function is also shown below: