We are given the system of equations;

Note that none of the variables has a coefficient of 1. All coefficients are greater than 1.
Therefore we would use the elimination method to solve this system of equations. To do this we would take one of the variables and then use its coefficients to multiply each equation in the reverse order. That is;
If we take the coefficient of x, then we shall multiply equation (1) by 2, and then multiply equation (2) by 6.
This is shown below;

We simplify this and we now have;
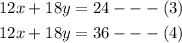
We now subtract equation (3) from (4);
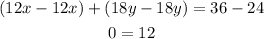
As we can see, this is not possible as we cannot have zero equals 12. There is no solution for this system of equations.