ANSWER
The width of the rectangle is 4.5ft
The length of the rectangle is 10ft
Step-by-step explanation:
Given information
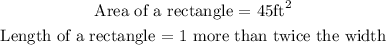
To find the dimension of the rectangle, follow the steps below
Step 1: Write the formula for calculating the area of a rectangle
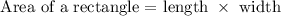
Step 2: Express the length of the rectangle in algebraic form
The length of the rectangle is 1 more than twice the width
Algebraically,
l = 2w + 1
l = 2w + 1
Step 3: Substitute the given data into the formula in step 1
![\begin{gathered} \text{ Area of the rectangle = length }*\text{ width} \\ \text{ Area = 45ft}^2 \\ \text{ 45 = \lparen2w + 1\rparen}*\text{ w} \\ \text{ open the parenthesis} \\ \text{ 45 = 2w}^2\text{+ w} \\ \text{ 2w}^2\text{ + w - 45 = 0} \end{gathered}]()
Step 4: Solve the quadratic function in step 3 using the general method

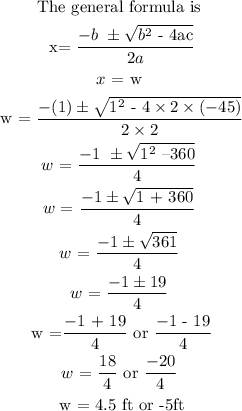
Hence, the width of the rectangle is 4.5ft
Step 5: Find the length of the width by putting w = 4.5
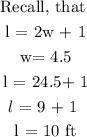
Hence, the length of the rectangle is 10ft