Question

The amount of pollutants that are found in waterways near large cities is normally distributed with mean 8.6 ppm and standard deviation 1.6 ppm. 39 randomly selected large cities are studied. Round all answers to 4 decimal places where possible.What is the distribution of X ? X ~ N(8.6,1.6)What is the distribution of ¯x ? ¯x ~ N(8.6,0.2562)What is the probability that one randomly selected city's waterway will have less than 9.5 ppm pollutants? For the 39 cities, find the probability that the average amount of pollutants is less than 9.5 ppm. For part d), is the assumption that the distribution is normal necessary? Yes NoFind the IQR for the average of 39 cities.Q1 = ppmQ3 = ppmIQR: ppm

Answer 1

b) We have to define the distribution for the sample mean.

The mean for the sampling distribution will be the same as the population mean, but the standard deviation will be affected by the sample size:

`\begin{gathered} \mu_s=\mu=8.6 \\ \sigma__s=(\sigma)/(√(n))=(1.6)/(√(39))\approx(1.6)/(6.245)\approx0.2562 \end{gathered}`

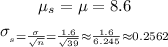
Then, the distribution is N(8.6, 0.2562).

c) We have to calculate the probability that a randomly chosen city have less than 9.5 ppm pollutants.

In this case, we have to use the populations distribution.

We start by calculating the z-score:

`z=(X-\mu)/(\sigma)=(9.5-8.6)/(1.6)=(0.9)/(1.6)=0.5625`

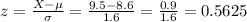
Then, we use this z-score to find the probability in the standard normal variable:

`P(X<9.5)=P(z<0.5625)=0.7131`

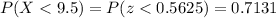
d) We now have to calculate the probability for the average of the 39 cities to have less than 9.5 ppm.

In this case, we use the sampling distribution, so we calculate the corresponding z-score as:

`z=(M-\mu_s)/(\sigma_s)=(9.5-8.6)/(0.2562)=(0.9)/(0.2562)\approx3.51288`

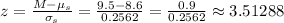
Now we can express the probability as:

`P(M<9.5)=P(z<3.51288)=0.9998`

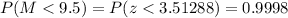
e) For sampling distributions, if the sample is large enough, we don't need to check for normality in the underlying distribution.

In this case, as the underlying distribution is normal, the sample size can be small and still have a normal distribution for the sampling distribution.

f) We have to calculate Q1, Q3 and IQR.

We can use the z-scores for this quartiles and convert them back to the sampling distribution parameters.

The z-scores are:

`\begin{gathered} z_(q1)=-0.67449 \\ z_(q3)=0.67449 \end{gathered}`

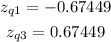
We then can calculate the quartiles as:

`\begin{gathered} Q_1=\mu_s+z_(q1)\sigma_s=8.6+(-0.67449)(0.2562)=8.6-0.1728=8.4272 \\ Q_3=\mu_s+z_q\sigma_s=8.6+(0.67449)(0.2562)=8.6+0.1728=8.7728 \end{gathered}`

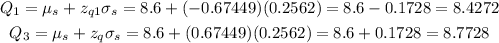
We can then calculate the IQR as:

`IQR=Q_3-Q_1=8.7728-8.4272=0.3456`

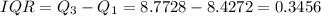
Answer:

b) N(8.6, 0.2562)

c) 0.7131

d) 0.9998

e) No

f) Q1 = 8.4272, Q3 = 8.7728, IQR = 0.3456