Answer:
m∠1=78°
m∠4=102°
Explanation:
Given: m∠6=102°
In the figure, angles 6 and 4 form an extended Z-shape. Thus, angles 6 and 4 are alternate angles.
Since alternate angles are equal in measure:
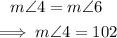
Next, angles 4 and 1 are on a straight line, therefore:

The measures of angles 1 and 4 are 78 degrees and 102 degrees respectively.