Question

Mr. Morales drove 360 miles to a conference. He had transmission problems on the return trip and it took him 3 hours longer at an average speed of 20 mph less than the trip going. What was his average speed on the return trip?

Answer 1

Step-by-step explanation

In the question, we are told that Mr. Morales drove 360 miles to a conference. He had transmission problems on the return trip and it took him 3 hours longer at an average speed of 20 mph less than the trip going.

We can break the above information into two equations using the formula for speed.

Recall,

`\text{Speed}=\text{ }\frac{\text{distance}}{Time}`

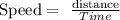
During the first trip we will have

`s=(360)/(t)----i`

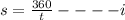
During the second trip we will have;

`s-20=(360)/(t+3)-----ii`

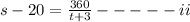
We can substitute equation i in ii

`\begin{gathered} (360)/(t)-20=(360)/(t+3|) \\ \text{Multiply through by t(t+3)} \\ 360(t+3)-20t(t+3)=360t \\ 360t+1080-20t^2-60t=360t \\ 20t^2+60t-1080=0 \\ \text{Divide through by 20} \\ t^2+3t-54=0 \\ t^2+9t-6t-54=0 \\ t(t+9)-6(t+9)=0 \\ (t-6)(t+9)=0 \\ t=6\text{ or t=-9} \end{gathered}`

Since time cannot be negative, t becomes 6 hours. Substituting t=6hours in equation i, we will have;

`s=(360)/(6)=60\text{mph}`

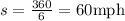
But since the average speed on the return trip is 20 mph less than the starting speed, the return speed becomes;

`\text{Return sp}eed\text{ = 60mph -20mph = 40 mph}`

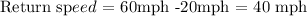
Answer: 40 mph