Question

Solve for x. ln(2x-2) - ln(x-1)= ln x

Answer 1

Remember the following property of logarithms:

`\ln (a)-\ln (b)=\ln ((a)/(b))`

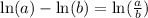
Use this property to simplify the left member of the equation and solve for x:

`\begin{gathered} \ln (2x-2)-\ln (x-1)=\ln (x) \\ \Rightarrow\ln ((2x-2)/(x-1))=\ln (x) \\ \Rightarrow(2x-2)/(x-1)=x \\ \Rightarrow2x-2=x(x-1) \\ \Rightarrow2(x-1)=x(x-1) \end{gathered}`

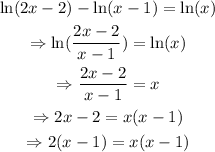
Since the factor (x-1) appears at both sides of the equation, we can simplify it as long as x is different from 1 (since the factor should not be equal to 0). Then:

`x=2`

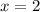
Plug in x=2 into the original equation to check the solution:

`\begin{gathered} \ln (2(2)-2)-\ln (2-1)=\ln (2) \\ \Rightarrow\ln (4-2)-\ln (1)=\ln (2) \\ \Rightarrow\ln (2)-\ln (1)=\ln (2) \end{gathered}`

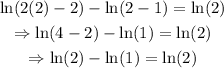
Since ln(1)=0, then:

`\ln (2)=\ln (2)`

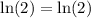
Therefore, the solution is x=2.