Here, we must find the derivative of

Using the method of differentiation, we can solve it using the limit:

We can use the four-step rule, it's the same thing as calculating the limit, we just break it into more steps. First, we take the original expression and replace "x" with "x + Δx"
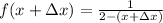
Now we subtract the original function from it
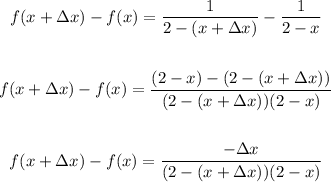
Now we divide both sides by Δx
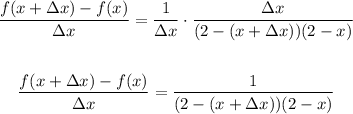
Now we can do the limit when Δx→0
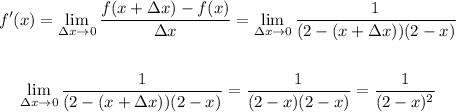
Therefore the derivative is
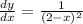
But the exercise doesn't end here, we must find when the derivative is equal to 1/16, therefore:
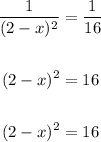
Hence
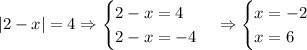
Therefore, the values of x that satisfies the problem are x = -2 and x = 6