Given: A quadratic equation
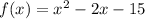
Required: To find the vertex, x-intercepts, y-intercept, and graph the given quadratic function.
Explanation: Comparing the given equation with general quadratic function
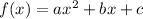
we get, a=1, b=-2, and c=-15. Now the x coordinate of the vertex of the quadratic function is

Hence,
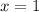
At x=1, f(x) is

Hence the vertex of the given function is (1,-16). Now for getting the x-intercept we put f(x)=0, i.e.,
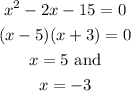
Hence the x-intercepts are (5,0) and (-3,0). Similarly, for y-intercept, we put x=0 and find f(x) as follows
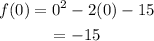
Hence y-intercept is (0,-15). Now using the vertex and intercepts to graph the given quadratic function is shown below.
Final Answer: b) Vertex=(1,-16)
c) x intercepts are (5,0) and (-3,0)
d) y intercepts is (0,-15)
e) The graph of f(x) is shown below.