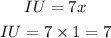Solution
- The triangle RTU is congruent to triangle RIU.
- This is because both triangles have a common side RU. They also have two equal angles, 19 degrees. Lastly, they also have RT = RI, given in the question.
- Thus, based on the Side-Angle-Side congruency, both triangles are equal.
- Thus, since TU and UI are the corresponding sides of both triangles, we can as well equate them.
- This is done below:

- Thus, the segment IU is: