This is a problem of similar triangles, then let's make a sketch of the situation:
Then, those triangles are similar, then if we call x the height of the tree, the theorem of similar triangles states:
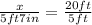
First let's convert 5ft7in to feet:
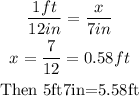
Now, let's solve for x:
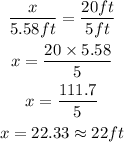
Then the height of the tree is 22 ft