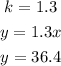From the statement of the problem we know that y is proportional to x, so the equation of y in terms of the variable x, constitutes a linear equation of the form:
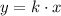
Where k is the slope.
1) We also know that for y = 5.2 the variable x takes the value x = 4, replacing these in the equation above we have:
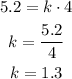
2) Replacing the value of k in the first equation we get:
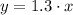
3) Now, given the last equation and a value x = 28 we find the value for y:
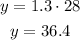
In summary, the answers are: