Question

can you help me with this? i’m not too sure how to start. Write a system of equations to describe the situation below, solve using augmented matrix, and fill in the blanks. This morning, Arianna processed two catering orders at the sandwich shop where she works The first order was for 9 trays of club sandwiches and 3 trays of vegetarian sandwiches, at a cost of $57. The second order, which cost $5, was for 1 tray of club sandwiches. How much do the trays cost? A tray of club sandwiches costs ($?) and a tray of vegetarian sandwiches cost ($?).

Answer 1

A tray of club sandwiches costs $4.67

A tray of vegetarian sandwiches costs $5.

Explanation:

Let x be a tray of club sandwiches costs and y be a tray of vegetarian sandwiches cost.

We create the matrix:

`\begin{pmatrix}9&3\\ \:\:0&1\end{pmatrix}\cdot \begin{pmatrix}x\\ \:y\end{pmatrix}=\begin{pmatrix}57\\ \:\:5\end{pmatrix}`

We solve the matrix, just like this:

`\begin{gathered} \begin{pmatrix}9x+3y \\ 0\cdot\:x+1\cdot\:y\end{pmatrix}=\begin{pmatrix}57 \\ \:\:5\end{pmatrix} \\ \begin{pmatrix}9x+3y\\ y\end{pmatrix}=\begin{pmatrix}57\\ 5\end{pmatrix} \\ \begin{bmatrix}y=5\end{bmatrix}\rightarrow y=\text{ \$5} \\ \begin{bmatrix}9x+3\cdot\:5=57\end{bmatrix}\rightarrow\begin{bmatrix}9x+15=57\end{bmatrix}\rightarrow\begin{bmatrix}9x=57-15\end{bmatrix}\rightarrow\begin{bmatrix}x=(42)/(9)\end{bmatrix}\rightarrow\begin{bmatrix}x=(14)/(3)\end{bmatrix}\rightarrow x=\text{ \$4.67} \end{gathered}`

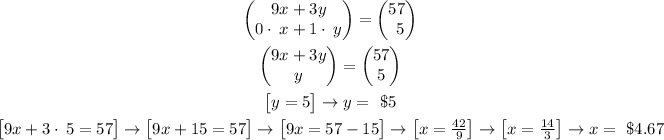
Therefore:

A tray of club sandwiches costs $4.67 and a tray of vegetarian sandwiches costs $5.