ANSWER:
A tray of club sandwiches costs $4.67
A tray of vegetarian sandwiches costs $5.
Explanation:
Let x be a tray of club sandwiches costs and y be a tray of vegetarian sandwiches cost.
We create the matrix:
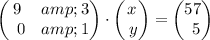
We solve the matrix, just like this:
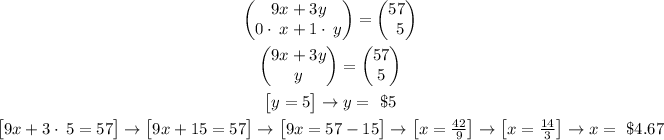
Therefore:
A tray of club sandwiches costs $4.67 and a tray of vegetarian sandwiches costs $5.