We want to find out how long it takes a ball to hit the ground using a quadratic function.
Typically, we can do this by finding the x-intercepts, or zeros of the function.
We are given the function:
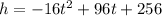
Since we want to know when the ball hits the ground, we will let the height of the ball be h = 0.
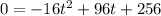
Any method can be helpful here:
- factoring
- completing the square
- quadratic formula
For this, we can use the factoring method. To begin, let's divide out the greatest common factor:
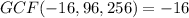
We get:
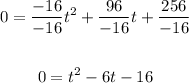
Next, we want to find two factors of -16 that add to give us -6.
We would get -8 and 2. We can use those to separate the middle term:
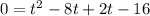
Grouping the first two and last two terms gives us:
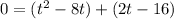
We can factor out a t from the first set, and 2 from the second set, like this:
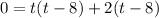
Finishing the factoring method, we have:
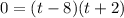
Next, we apply the zero product property to solve for each factor:
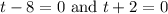
From the first factor, we get:
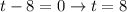
For the second factor:
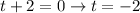
Since this is a real world situation, we need to keep the positive value.
Therefore, we will use t = 8. We interpret this as, "It takes 8 seconds for the ball to hit the ground."