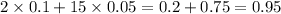Question

Matthew has a dimes and y nickels. He has at least 15 coins worth a maximum of $1 combined. Solve this system of inequalities graphically and determine one possible solution

Answer 1

Since the number of dimes is x and the number of nickels is y, then the total number of coins is x+y. Since Matthew has at least 15 coins, then:

`\begin{gathered} 15\le x+y \\ \Rightarrow15-x\le y \\ \Rightarrow y\ge15-x \end{gathered}`

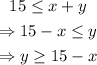
Since a dime has a value of 0.1 and a nickel has a value of 0.05, the total value of x dimes is 0.1x and the total value of y nickels is 0.05y. Furthermore, since Matthew's coins have a maximum value of $1 combined, then:

`\begin{gathered} 0.1x+0.05y\le1 \\ \Rightarrow0.05y\le1-0.1x \\ \Rightarrow y\le(1)/(0.05)-(0.1x)/(0.05) \\ \Rightarrow y\le20-2x \end{gathered}`

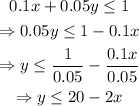
Then, the system of inequalities is:

`\begin{gathered} y\ge15-x \\ y\le10-2x \end{gathered}`

Plot the system to solve it graphically:

The green region is the solution for both inequalities simultaneously.

Since the number of coins must be positive, then the solution must lie on the first quadrant of the coordinate plane:

Pick any point inside the green region. That is a possible solution:

Then, a possible solution is x=2 and y=15.

This way, the total number of coins is 17 and the total value of those coins is:

`2*0.1+15*0.05=0.2+0.75=0.95`