Question

ParagraphAdobe Acrobat1. A football is kicked at ground level with an initial velocity of 64 feet per second.1. standard form: y = -167 +64IV. Graph:II. vertex form: y--161 - 2) + 64SHIRIIII. intercept form: y = -1611 - 4)a. To find the maximum height of the football.Form: (choose) Explanation:I II III IVb. To find the height after 3 secondsExplanation:Form: (choose)I II III IVC. To find the time when the football hits the ground.Form: (choose)Explanation:I II III IV

Answer 1

Given the equation below,

`y=-16t^2+64t`

To find the maximum point, dy/dt = 0.

Differentiating the equation above,

`\begin{gathered} y=-16t^2+64t \\ (dy)/(dt)=-32t+64 \end{gathered}`

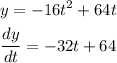
Where dy/dt = 0,

`\begin{gathered} -32t+64=0 \\ -32t=-64 \\ t=(-64)/(-32)=2 \end{gathered}`

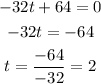
Substituting for t into the equation, maximum height is'

`\begin{gathered} y=-16t^2+64t \\ \text{Where t = 2} \\ y=-16(2)^2+64(2) \\ y=-16(4)+128_{} \\ y=-64+128=64 \end{gathered}`

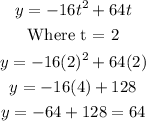
Hence, the maximum height of the football is 64 ft.

The vertex form is to be used which is given below as,

`y=-16(t-2)^2+64`

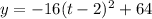
Where (h, k) represents the coordinate of the vertex and k is the maximum height.