Given the equation below,
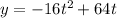
To find the maximum point, dy/dt = 0.
Differentiating the equation above,
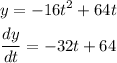
Where dy/dt = 0,
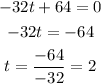
Substituting for t into the equation, maximum height is'
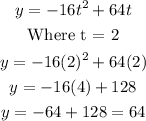
Hence, the maximum height of the football is 64 ft.
The vertex form is to be used which is given below as,
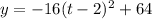
Where (h, k) represents the coordinate of the vertex and k is the maximum height.