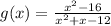Question

The domain of function G is (-oo,-4) u (-4,3) u (3,oo) and as X approaches either -oo or oo, The value of the function approaches 1. Which equation could represent function G

Answer 1

Domain of g: (-∞,-4)u(-4,3)u(3,∞)

The domain of a rational function is the set of all real numbers except the zeros of the denominator. Then, the zeros of the denominator of g are -4 and 3.

Denominator of g:

`(x+4)(x-3)`

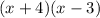
Simplify:

`\begin{gathered} (x+4)(x-3)=x\cdot x-3\cdot x+4\cdot x-3\cdot4 \\ \\ (x+4)(x-3)=x^2-3x+4x-12 \\ \\ (x+4)(x-3)=x^2+x-12 \end{gathered}`

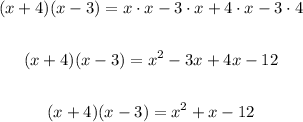
Horizontal asymptore: as x approaches either -∞ or ∞, the value of the function approaches 1.

The horizontal asymptote y=1 indicates that the ratio of leading coefficients of numerator and denominator is 1 (numerator and denominator have the same degree). As the leading coefficient of denominator is 1, then the leading coefficient of the numerator is also 1. Both, numerator and denominator are degree 2.

Then, the function g is:

`g(x)=(x^2-16)/(x^2+x-12)`