If triangle ABC was dilated to triangle AXY, with A as the center of dilation, then
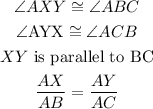
Having known that the center of dilation is point A, then we can conclude that line AB is dilated to line AX in the same ration that line AC is dilated to line AY.
Since its a dilation from one shape to the other, then line XY must be parallel to line BC. Since both lines are parallel, the angle formed at angle ABC is the same as that formed by angle AXY.
The same rule applies to angles ACB and AYX.
Also, since ABC and AXY are similar triangles, then the ratio AX over AB = AY over AC is applicable