Answer
The height of the lightning rod = 27.37 ft
Step-by-step explanation
The given parameters can be represented as shown in the figure below:
What to find:
The height of the lightning rod, h₁.
Step-by-step solution:
The height of the lightning rod, h₁ can be calculated using h₁ = H - h₂
Using trigonometric function
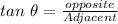
To find h₂,
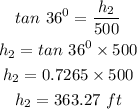
To find H,
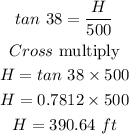
Since h₂ = 363.27 ft, and H = 390.64 ft, then
h₁ = 390.64 ft - 363.27 ft = 27.37 ft