First, we can see in the alternatives that the base of the logarithm is not changed, so we don't need to bother with that.
Now, a multiplication inside a logarithm has the following property:
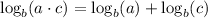
Applying that to the given expression, we have:
![\log _3(\sqrt[5]{x}\cdot y)=\log _3(\sqrt[5]{x})+\log _3y](https://img.qammunity.org/2023/formulas/mathematics/college/30qzwgkc0w4sjfa22xunq502gclcvead3x.png)
Now, we can rewrite the root in the radical form:
![\sqrt[5]{x}=x^{(1)/(5)}](https://img.qammunity.org/2023/formulas/mathematics/college/embnspw2p3wtv4nz75kkandw92bd8ab8kv.png)
To get:
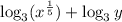
We did that so we can use the following property:
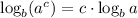
Let's do that:
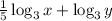
And that is the answer.