The confidence interval is given by
![\begin{gathered} \bar{x}\pm z*\frac{\sigma}{\sqrt[]{n}} \\ \text{ Where} \\ \bar{x}=\text{ the sample mean} \\ z=\text{ the z-score} \\ \sigma=\text{ the standard deviation} \\ n=\text{ the sample size} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y8nivc4v247foyzfkyjxej0stymjxmmepw.png)
We will now find the alpha level, α.
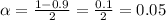
The z-score for a 90% confidence interval is 1.645.
The question gives the margin of error as 2.4 lb.
Therefore,
![2.4=z*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/1eri3gvherhrmkzsx4mnqku775gsrx2tn4.png)
Substituting the values, we get
![2.4=1.645*\frac{23}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/66geuhgbc8ua2vzu4nce7p13eoccz34hwk.png)
Making n the subject of formula:
![\begin{gathered} \sqrt[]{n}=(1.645*23)/(2.4) \\ \sqrt[]{n}=(37.835)/(2.4)=15.685 \\ \therefore \\ n=15.685^2 \\ n=246 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wq0r0gjgzozl45aupxtzz0agchngub9z34.png)
The sample size is 246.