Given:
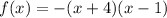
Step-by-step explanation:
a) To draw: The Graph
Let us find the intercepts.
When x = 0, we get
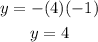
Therefore, the y-intercept is (0, 4).
The x-intercepts are,
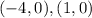
Let us find the vertex.
The given function can be written as,
![\begin{gathered} f(x)=-(x+4)(x-1) \\ =-(x^2+3x-4) \\ =-(x^2+3x+((3)/(2))^2-((3)/(2))^2-4) \\ =-[(x+(3)/(2))^2-(9)/(4)-4] \\ =-[(x+(3)/(2))^2-(25)/(4)] \\ f(x)=(x+(3)/(2))^2+(25)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4nxli0sjglse63wq3e0dk99tiozu9i6geo.png)
So, the vertex is,
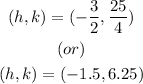
The graph becomes,
b) The equation of symmetry is,
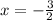
This line divides the parabola into two equal parts.
c) The coordinates of the vertex is,
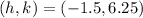
d) Intercepts:
The x-intercepts are,
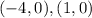
The y-intercept is (0, 4).