Question

I need to know how to do the whole thing and understand it.

Answer 1

We are given the data on the number of candies handed by neighborhood A and neighborhood B.

Let us first find the mean and variance of each neighborhood.

Mean:

`\bar{x}_A=(\sum x)/(N_1)=(12)/(6)=2`
`\bar{x}_B=(\sum x)/(N_2)=(20)/(6)=3.33`

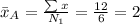
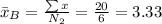
Variance:

`s_A^2=(\sum x^2)/(N_1)-\bar{x}_A^2=(28)/(6)-2^2=0.667`
`s_B^2=(\sum x^2)/(N_2)-\bar{x}_B^2=(80)/(6)-3.33^2=2.244`

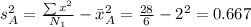
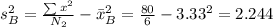
A. Null hypothesis:

The null hypothesis is that there is no difference in the mean number of candies handed out by neighborhoods A and B.

`H_0:\;\mu_A=\mu_B`

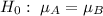
Research hypothesis:

The research hypothesis is that the mean number of candies handed out by neighborhood A is more than neighborhood B.

`H_a:\;\mu_A>\mu_B`

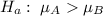
Test statistic (t):

The test statistic of a two-sample t-test is given by

`t=\frac{\bar{x}_A-\bar{x}_B}{s_p}`

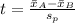
Where sp is the pooled standard deviation given by

`\begin{gathered} s_p=\sqrt{(N_1s_1^2+N_2s_2^2)/(N_1+N_2-2)((N_1+N_2)/(N_1\cdot N_2)}) \\ s_p=\sqrt{(6\cdot0.667+6\cdot2.244)/(6+6-2)((6+6)/(6\cdot6))} \\ s_p=0.763 \end{gathered}`
`t=(2-3.33)/(0.763)=-1.74`

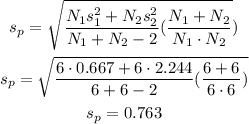
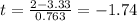
So, the test statistic is -1.74

Critical t:

Degree of freedom = N1 + N2 - 2 = 6+6-2 = 10

Level of significance = 0.05

The right-tailed critical value for α = 0.05 and df = 10 is found to be 1.81

Critical t = 1.81

We will reject the null hypothesis because the calculated t-value is less than the critical value.

Interpretation:

This means that we do not have enough evidence to conclude that neighborhood A gives out more candies than neighborhood B.