Question

A carpenter is building a unique jewelry box in the shape of a right triangular prism with the dimensions shown below. How much wood will it take to complete the project?

Answer 1

The carpenter will need 30 cubic inches of wood to complete the project.

The volume of a triangular prism is equal to the area of the base
`$*$` depth.

In this case, the area of the base is
`$(1)/(2)$` base
`$*$` height and from the image we can find that the base is 4 in and the height is 3 in.

So the area of the base is
`$(1)/(2) 4 \mathrm{in} * 3 \mathrm{in}=6 \mathrm{in}^2$`.

From the image, we can then find that the depth is 5 in.

Therefore, the total volume of the prism is
`$6 \mathrm{in}^2 * 5 \mathrm{in}=30 \mathrm{in}^3$`.

So the carpenter will need 30 cubic inches of wood to complete the project.

Answer 2

To determine how much wood the carpenter will need we have to find the surface area of the jewelry box. To do this we need to notice that the box is made of:

• Two traingles with base 3 in and height 4 in.

,

• One rectangle with length 5 in and width 2 in.

,

• One rectangle with length 3 in and width 2 in.

,

• One rectangle with length 4 in and width 2 in.

Now, we find tha area of each part of the box and add them to get the surface area.

The area of a triangle is given by:

`A_T=(1)/(2)bh`

The area of a rectangle is given by:

`A_R=lw`

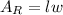
Hence the total area is given by:

`\begin{gathered} A=2\cdot(1)/(2)(3)(4)+(5)(2)+(3)(2)+(4)(2) \\ A=36 \end{gathered}`

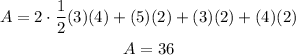
Therefore, the carpenter will need 36 square inches of wood.