as you can see on the following draw:
each triangle is right and isosceles. so we can use Pythagoras and find out the length of each side of the triangle, which is the radius of the circle:
![\begin{gathered} h^2=r^2+r^2 \\ h=6 \\ 6^2=r^2+r^2 \\ 36=2r^2 \\ (36)/(2)=r^2 \\ 18=r^2 \\ r=\sqrt[]{18}\approx4.24 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i7wua9z3zuoatiyru70q5v5vdb7z42m8p2.png)
and the area of the circle is:
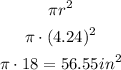
so the answer is: 18π square inches