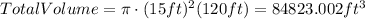Question

2. The holding tanks are congruent in size, and both are in the shape of a cylinder that has been cut in half vertically. The bottom of the tankis a curved surface. What is the volume of both tanks if the radius of tank #1 is 15 feet and the height of tank #2 is 120 feet? You mustexplain your answer using words, and you must show all work and calculations to receive creditx

Answer 1

So,

Congruent tanks implies that both tanks are of identifical shape, form & dimensions. Congruent means that the tanks have the same radius as well as height. Hence, the heights and radius of tanks #1 and #2 are equal and the same.

Now:

- radius(tank #1) = 15 ft ⇒ radius(tank #2) = 15 ft

- height(tank #2) = 120 ft ⇒ height(tank #1) = 120 ft

The volume of a cylinder is given by the equation:

`V=\pi\cdot r^2\cdot h`

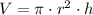
As the tanks have been cut into half, we got that the volume of each tank is:

`V=(1)/(2)\pi\cdot r^2\cdot h`

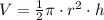
The volume of both tanks is the sum of the volume each one, so:

`\text{TotalVolume=VTank1+Vtank2}_{}`

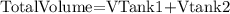
Both are cogruent so we could write:

`\text{Total}=(1)/(2)\pi\cdot r^2\cdot h+(1)/(2)\pi\cdot r^2\cdot h=\pi\cdot r^2\cdot h`

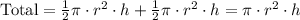
If we replace:

`TotalVolume=\pi\cdot(15ft)^2(120ft)=84823.002ft^3`