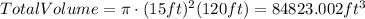So,
Congruent tanks implies that both tanks are of identifical shape, form & dimensions. Congruent means that the tanks have the same radius as well as height. Hence, the heights and radius of tanks #1 and #2 are equal and the same.
Now:
- radius(tank #1) = 15 ft ⇒ radius(tank #2) = 15 ft
- height(tank #2) = 120 ft ⇒ height(tank #1) = 120 ft
The volume of a cylinder is given by the equation:

As the tanks have been cut into half, we got that the volume of each tank is:
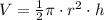
The volume of both tanks is the sum of the volume each one, so:

Both are cogruent so we could write:
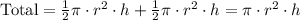
If we replace: