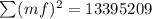Used data below to complete the following calculations m=65,37,6,

Question

asked Oct 19, 2023 153k views

1 Answer

Swisher Sweet · Answer 1 · 2023-10-24T20:42:17+0000

we are given a data set and we are asked to determine the following operations:

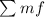
$\sum ^{}_{}mf$

To determine this, we need to add the products of each of the values of "m" and "f", like this:

$\sum ^{}_{}mf=m_1f_1+m_2f_2+m_3f_3+m_4f_4+m_5f_5$

Replacing the values:

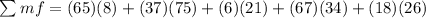
$\sum ^{}_{}mf=(65)(8)_{}+(37)(75)+(6)(21)+(67)(34)+(18)(26)$

Solving the operation:

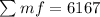
$\sum ^{}_{}mf=6167$

Now we are asked to determine the following operation:

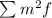
$\sum ^{}_{}m^2f$

Now we need to add the product of the squares of "m" by "f", like this:

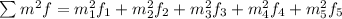
$\sum ^{}_{}m^2f=m^2_1f_1+m^2_2f_2+m^2_3f_3+m^2_4f_4+m^2_5f_5$

replacing the values:

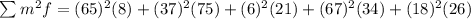
$\sum ^{}_{}m^2f=(65)^2(8)_{}+(37)^2(75)+(6)^2(21)+(67)^2(34)+(18)^2(26)$

Solving the operations we get:

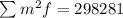
$\sum ^{}_{}m^2f=298281$

Now we are asked to solve the following operation:

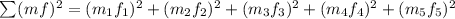
$\sum ^{}_{}(m^{}f)^2=(m_1f_1)^2+(m_2f_2)^2+(m_3f_3)^2+(m_4f_4)^2+(m_5f_5)^2$

Replacing the values we get:

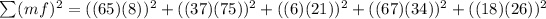
$\sum ^{}_{}(m^{}f)^2=((65)(8)_{})^2+((37)(75))^2+((6)(21))^2+((67)(34))^2+((18)(26))^2$

Solving we get:

$\sum ^{}_{}(m^{}f)^2=13395209$