Question

Determine the number of term for each given arithmetic series.

Answer 1

a₁ = 4.2

aₙ = 52.2

sₙ = 366.6

Using the formulars

aₙ = a₁ + (n-1) d

52.2 = 4.2 + (n-1)d ------------------------(1)

Also,

`S_{n\text{ }}=(n)/(2)\lbrack2a_1\text{ + (n-1)d\rbrack}`

`366.6=(n)/(2)\lbrack2(4.2)\text{ + (n-1)d \rbrack}`

`366.6\text{ =}(n)/(2)\lbrack8.4\text{ + (n}-1)d\text{ \rbrack}`

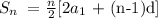
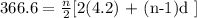
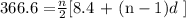
From equation(1), 52.2 - 4.2 = (n-1)d, this implies; (n - 1)d = 48

substitute (n-1)d = 48 in the above

`366.6\text{ =}(n)/(2)\lbrack8.4\text{ + 48\rbrack}`

`366.6\text{ =}(n)/(2)(56.4)`

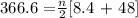
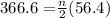
Multiply both-side by 2

733.2 = 56.4 n

Divide both-side of the equation by 56.4

n = 13

Hence, the number of term is 13