a₁ = 4.2
aₙ = 52.2
sₙ = 366.6
Using the formulars
aₙ = a₁ + (n-1) d
52.2 = 4.2 + (n-1)d ------------------------(1)
Also,
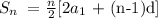
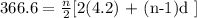
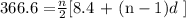
From equation(1), 52.2 - 4.2 = (n-1)d, this implies; (n - 1)d = 48
substitute (n-1)d = 48 in the above
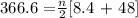
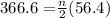
Multiply both-side by 2
733.2 = 56.4 n
Divide both-side of the equation by 56.4
n = 13
Hence, the number of term is 13